2. RISPOSTA SISMICA DI BLOCCHI RIGIDI
D. Liberatore1, G. Spera1
1 DiSGG, Università degli Studi della Basilicata
|
2. RISPOSTA SISMICA DI BLOCCHI RIGIDI |
|
2.1 Premessa |
|
2.2 Bacini di attrazione del blocco |
|
2.3 Funzioni di ribaltamento |
|
2.3.1 Energia totale modificata |
|
2.3.2 Differenza in velocità angolare |
|
2.3.3 Prodotto in velocità angolare |
|
2.3.4 Confronto tra le funzioni di ribaltamento |
|
2.4 Funzioni di ribaltamento in presenza di un'azione sismica |
|
2.5 Funzionale di ribaltamento |
|
2.5.1 Applicazione ad una colonna dell'Incompiuta di Venosa |
|
2.6 Conclusioni |
2.1 Premessa
La vulnerabilità degli elementi strutturali incompleti e/o a blocchi, caratterizzati da elevata snellezza, è strettamente legata a un comportamento dinamico fortemente non lineare, sia per materiale che per geometria, ed è difficilmente valutabile attraverso analisi statiche. Il meccanismo di collasso più frequente sotto azioni sismiche è quello del ribaltamento, sia nel caso di strutture murarie, ad es. pareti isolate o con scarso ammorsamento con pareti ortogonali, sia nel caso di sistemi a blocchi, come le colonne. A ciò deve aggiungersi l'eventuale presenza di strutture spingenti, come archi e volte.
La risposta dinamica di un blocco soggetto a un'azione sismica presenta tre possibili esiti: a) il blocco non oscilla; b) il blocco oscilla senza ribaltare; c) il blocco oscilla e ribalta. La natura discreta dell'esito della risposta costituisce una delle maggiori difficoltà nella definizione di indici sintetici di ribaltamento.
Una possibile strada per la ricerca di tali indici consiste nell'esprimere la tendenza del blocco al ribaltamento attraverso grandezze continue con un valore di soglia in corrispondenza della posizione di equilibrio instabile e tali da ordinare monotonicamente situazioni caratterizzate da tendenza al ribaltamento via via più elevata.
2.2 Bacini di attrazione del blocco
Le grandezze caratteristiche del blocco sono il peso W, la larghezza b, l'altezza h, l'angolo a tra la verticale e la congiungente il baricentro G con lo spigolo di rotazione O, la snellezza m = h/b = cot a, la taglia R, il momento d'inerzia IO rispetto al punto O (Fig. 2.1). La rotazione del blocco, indicata con q, è assunta positiva se antioraria.
Si assume che l'attrito tra il blocco e il piano d'appoggio sia tale da impedire lo scorrimento; pertanto risulta possibile soltanto la rotazione del blocco attorno a uno dei due spigoli O e O'. Tale ipotesi risulta ben verificata per blocchi snelli, quali quelli di comune interesse ai fini del ribaltamento (Housner 1963).
L'equazione del moto per le oscillazioni libere del blocco è:
(1)
![]()
che, ponendo:
(2)
p2 = WR/IO
diventa:
(3)
![]()
Poiché:
(4)
![]()
l'equazione del moto può essere riscritta:
(5)
![]()
che, integrata, diventa:
(6)
![]()
La costante può essere calcolata dalle condizioni iniziali q(0) = q0, ![]()
(7)
![]()
che rappresenta la traiettoria nello spazio delle fasi per le assegnate condizioni iniziali.
Lo stesso risultato poteva ottenersi uguagliando l'energia totale nella posizione iniziale e nella generica posizione ruotata.
Nella Fig. 2.2 è riportato il ritratto di fase di un blocco con µ = 2 e p = 2.565; le traiettorie sono periodiche di p.
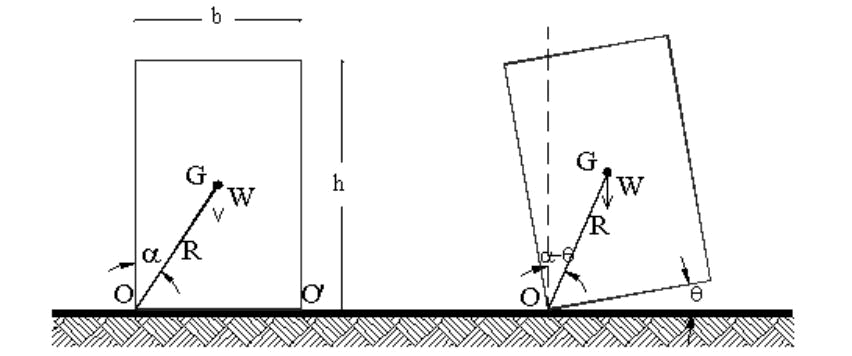
Fig. 2.1 - Blocco nella posizione di riferimento e nella posizione ruotata.
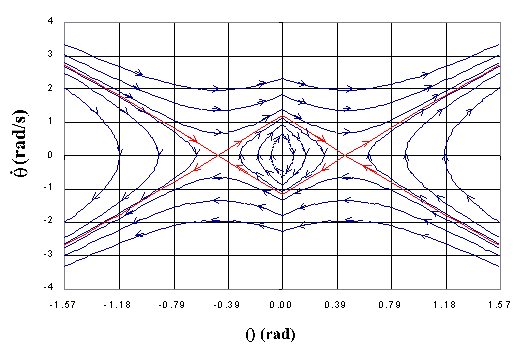
Fig. 2.2 - Ritratto di fase per un blocco con µ = 2 e p = 2.565.
Le energie potenziale e cinetica sono:
(8)
![]()
![]()
e l'energia totale:
(9)
![]()
Si studia ora la frontiera tra i bacini di attrazione della posizione di riferimento q = 0 e della posizione ribaltata a q = p/2.
Nella posizione di equilibrio instabile q = a, l'energia potenziale assume il valore WR, che coincide con il massimo dell'energia totale in assenza di ribaltamento.
Affinché il blocco raggiunga la posizione di equilibrio
instabile con velocità nulla, partendo da una rotazione iniziale 0 < q < a,
la velocità angolare iniziale, indicata con ![]()
(10)
![]()
da cui si ricava:
(11)
![]()
L'Equazione 11 rappresenta la frontiera tra i bacini di attrazione di q = 0 e di q = p/2, per una rotazione iniziale 0 < q < a.
La posizione di equilibrio instabile può essere raggiunta anche da una rotazione iniziale a < q < p/2, purché la velocità angolare iniziale del blocco sia negativa. Uguagliando l'energia totale a quella potenziale della posizione di equilibrio instabile si ricava:
(12)
![]()
Le Equazioni 11 e 12 possono essere sintetizzate nell'Equazione 13, di seguito riportata:
(13)
![]()
valida in tutto il campo 0 < q £ p/2.
Per rotazione iniziale negativa, la posizione di equilibrio
instabile q = a
può ancora essere raggiunta dopo un impatto con il piano d'appoggio. Definito
il coefficiente di restituzione come il rapporto tra le velocità angolari dopo
e prima dell'urto, indicate con ![]()
![]()
(14)
![]()
la velocità angolare immediatamente prima dell'urto risulta:
(15)
![]()
L'energia totale nel generico istante iniziale è uguale a quella immediatamente prima dell'urto:
(16)
![]()
da cui si ricava l'espressione della frontiera, valida per -p/2 £ q < 0:
(17)
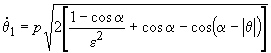
Ponendo:
(18)
![]()
le Equazioni 13 e 17 possono essere sintetizzate nell'Equazione 19, di seguito riportata, valida per -p/2 £ q £ p/2, q ¹ 0:
(19)
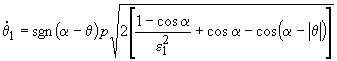
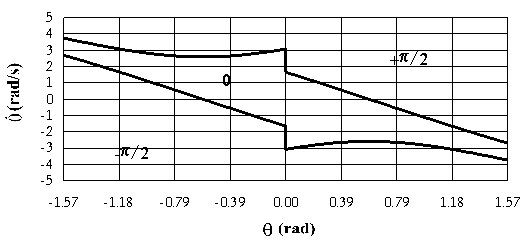
Fig. 2.3 - Bacini di attrazione per un blocco con µ = 1.5, p = 2.857, e = 0.5385.
La frontiera tra il bacino di q = 0 e quello di q = -p/2 è simmetrica alla precedente rispetto all'origine. Ponendo:
(20)
![]()
l'espressione della frontiera è:
(21)
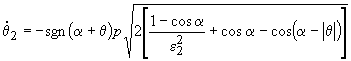
E' possibile sintetizzare le equazioni delle due frontiere in un'unica equazione, associando l'indice j = 1 alla frontiera tra i bacini di q = 0 e di q = p/2, e l'indice j = 2 alla frontiera tra i bacini di q = 0 e di q = -p/2:
(22)
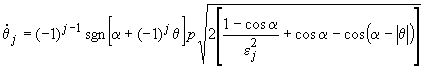 (j = 1,2)
(j = 1,2)
Nella posizione q = 0, le frontiere presentano una discontinuità, a causa dell'urto del blocco con il piano d'appoggio, e della corrispondente dissipazione di energia.
Nella Fig. 2.3, a titolo di esempio, sono mostrati i bacini di attrazione per un blocco con m = 1.5, p = 2.857, e = 0.5385.
2.3 Funzioni di ribaltamento
Noti i bacini di attrazione della posizione non ribaltata e
delle due posizioni ribaltate, è sufficiente verificare a quale bacino
appartenga il punto rappresentativo delle condizioni iniziali (q,
![]() ) per stabilire se il blocco ribalta o meno. Tuttavia, per
ordinare monotonicamente condizioni iniziali caratterizzate da tendenza al
ribaltamento via via più spiccata, è necessario definire un'unica grandezza,
funzione di q
e
) per stabilire se il blocco ribalta o meno. Tuttavia, per
ordinare monotonicamente condizioni iniziali caratterizzate da tendenza al
ribaltamento via via più spiccata, è necessario definire un'unica grandezza,
funzione di q
e ![]()
2.3.1 Energia totale modificata
Si considera, per semplicità, il caso q > 0, essendo il caso q < 0 simmetrico rispetto all'origine.
L'energia totale, adimensionalizzata rispetto al prodotto WR, è:
(23)
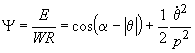
Sulla frontiera j = 1 si ha E = WR, e dunque l'energia totale adimensionalizzata assume il valore:
(24)
Y1 = 1
Sulla frontiera j = 2, si ha:
(25)
![]()
e l'energia adimensionalizzata assume il valore:
(26)
![]()
Il coefficiente di restituzione assume l'espressione, nell'ipotesi di urto totalmente anelastico (Giannini & Masiani 1991):
(27)
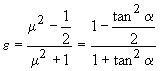
e l'energia adimensionalizzata dipende da a secondo l'espressione:
(28)
![]()
L'energia totale adimensionalizzata ha l'andamento riportato in Fig. 2.4.
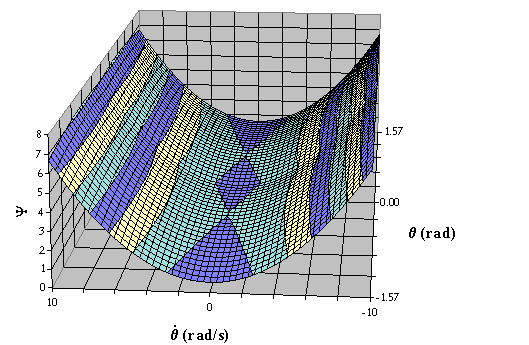
Fig. 2.4 - Energia totale adimensionalizzata.
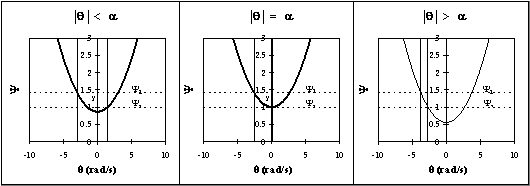
Fig. 2.5 - Sezioni a q = cost. dell'energia totale adimensionalizzata.
Una possibile definizione di funzione di ribaltamento può essere formulata imponendo che questa assuma valori minori di Y1 = 1 nel bacino di attrazione di q = p/2, valori compresi tra Y1 e Y2 nel bacino di attrazione di q = 0, valori maggiori di Y2 nel bacino di attrazione di q = -p/2.
L'energia totale adimensionalizzata non risponde a tali requisiti, come mostrato nella Fig. 2.5, che riporta diverse sezioni a q = cost. Infatti, per q < p, il bacino di q = 0, delimitato dalle due linee continue verticali, è caratterizzato da valori di Y anche minori di 1, e inoltre il bacino di q = p/2 è caratterizzato da valori di Y sempre maggiori di 1. Per q ³ a, invece, il bacino di q = p/2 è caratterizzato da valori di Y anche maggiori di 1.
Per formulare una funzione di ribaltamento che soddisfi le condizioni poste, è necessario modificare l'espressione dell'energia totale. La nuova grandezza, denominata brevemente Energia Totale Modificata (ETM) è:
(29)
![]()
in cui:
(30)
![]()
![]()
(31)
![]()
(32)
![]()
![]()
(33)
![]()
(34)
![]()
(35)
![]()
![]()
L'andamento dell'ETM è riportato in Fig. 2.6. In Fig. 2.7 sono riportate diverse sezioni a q = cost.
2.3.2 Differenza in velocità angolare
Una seconda funzione di ribaltamento può essere formulata osservando i diversi tipi di traiettoria nello spazio delle fasi (Fig. 2.8):
traiettoria diretta verso una posizione ribaltata, senza urti in corrispondenza di q = 0 (caso A);
traiettoria diretta verso una posizione ribaltata, con un urto in corrispondenza di q = 0 (caso B);
traiettoria diretta verso q = 0, con infiniti urti in corrispondenza di q = 0 (casi C e D).
L'andamento delle traiettorie suggerisce di definire la funzione di ribaltamento come la differenza in velocità angolare, con segno opportunamente scelto, tra un punto della traiettoria e il corrispondente punto di una delle due frontiere tra i bacini di attrazione (Fig. 2.9). In particolare, se la traiettoria è diretta verso una posizione ribaltata, senza urti (caso A), la differenza è presa in corrispondenza del punto iniziale; se invece la traiettoria comporta almeno un urto in corrispondenza di q = 0 (casi B, C e D), la differenza è presa immediatamente dopo il primo urto.
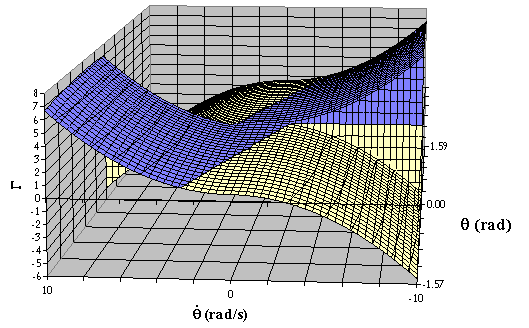
Fig. 2.6 - ETM.
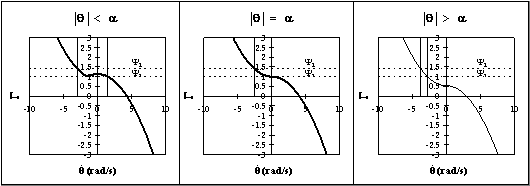
Fig. 2.7 - Sezioni a q = cost. dell'ETM.
Nel caso la traiettoria sia diretta verso una posizione ribaltata, senza urti, posto:
(36)
![]()
la frontiera rispetto alla quale calcolare la differenza in velocità angolare è:
(37)
![]()
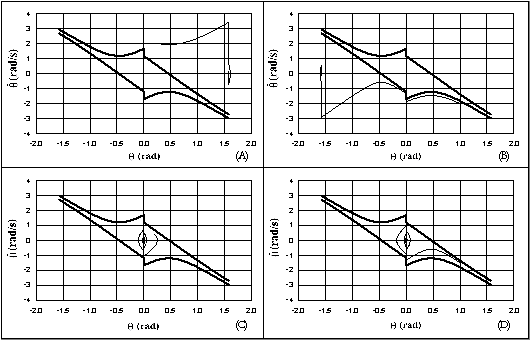
Fig. 2.8 - Tipi di traiettoria nello spazio delle fasi.
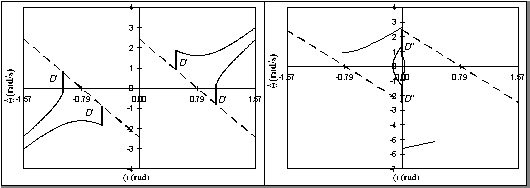
Fig. 2.9 - Differenza in velocità angolare per traiettorie senza urto e con urto.
L'Equazione 37 fornisce j = 1 per q
> 0 e j =
2 per q
< 0. Nel caso q
= 0, l'Equazione 37 fornisce j = 1 per
![]()
![]()
(38)
![]()
Nel caso la traiettoria comporti almeno un urto in
corrispondenza di q
= 0, indicata con ![]()
(39)
![]()
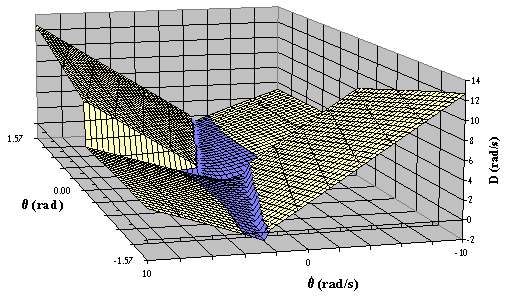
Fig. 2.10 - DVA.
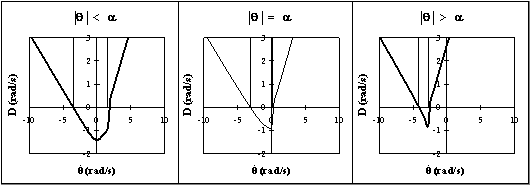
Fig. 2.11 - Sezioni a q = cost. della DVA.
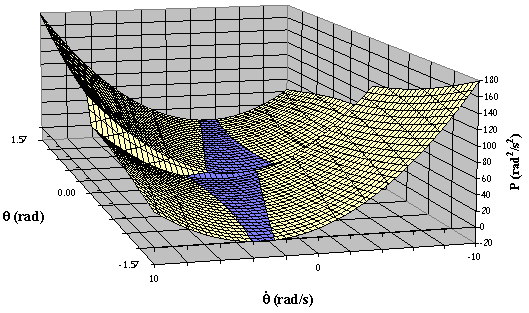
Fig. 2.12 - PVA.
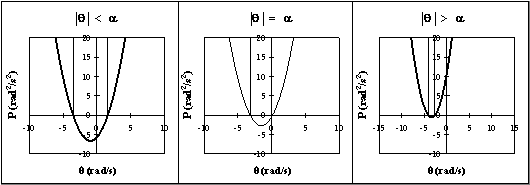
Fig. 2.13 - Sezioni a q = cost. della PVA.
La differenza in velocità angolare, in segno, ha l'espressione:
(40)
![]()
E' possibile fornire un'unica espressione della funzione di ribaltamento, denominata Differenza in Velocità Angolare (DVA), valida in entrambi i casi descritti:
(41)
![]()
in cui:
(42)
![]()
(43)
![]()
![]()
La DVA assume valori negativi nel bacino di attrazione di q = 0 e valori positivi nei bacini di attrazione di q = ±p/2 (Figg. 2.10 e 2.11).
2.3.3 Prodotto in velocità angolare
Una terza funzione di ribaltamento può essere definita come prodotto delle differenze in velocità angolare tra il punto iniziale della traiettoria e i corrispondenti punti delle due frontiere:
(44)
![]()
Questa funzione, indicata brevemente come Prodotto in Velocità Angolare (PVA), assume, analogamente alla DVA, valori negativi nel bacino di attrazione di q = 0 e valori positivi nei bacini di attrazione di q = ±p/2 (Figg. 2.12 e 2.13).
2.3.4 Confronto tra le funzioni di ribaltamento
Nella Figura 2.14 è riportata, a titolo di esempio, la
traiettoria di fase di un blocco con m= 1.5, p = 2.857, e
= 0.5385, in oscillazioni
libere a partire da una rotazione iniziale prossima a quella di equilibrio
instabile e da velocità angolare iniziale nulla. L'istante iniziale è
caratterizzato da un'ETM leggermente superiore a Y1 = 1, una DVA
pari a -0.764 rad/s e da un PVA leggermente inferiore a 0, a indicare che il blocco non
ribalta. Durante le oscillazioni libere, è possibile calcolare le funzioni di
ribaltamento a ogni istante, assumendo questo come l'istante iniziale delle
oscillazioni libere susseguenti (Fig. 2.14). Si osserva che l'ETM e la DVA
assumono valori costanti tra un urto e il successivo, mentra il PVA è
variabile. La successione dei valori dell'ETM è crescente e quella della DVA
decrescente. Il PVA, invece, non presenta un andamento monotono.
All'approssimarsi del blocco alla condizione q
= 0, ![]()
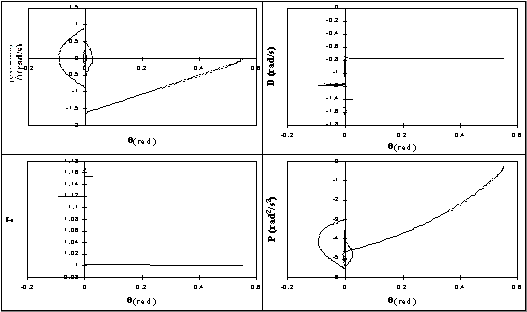
Fig. 2.14 - Traiettoria di fase per un blocco µ = 1.5, p = 2.857, e = 0.5385 e andamento delle funzioni di ribaltamento.
2.4 Funzioni di ribaltamento in presenza di un'azione sismica
Le funzioni di ribaltamento, ricavate nelle condizioni di oscillazioni libere, possono essere facilmente estese al caso di un'azione sismica. A questo scopo è sufficiente considerare, a ogni istante, la funzione di ribaltamento associata alla rotazione e alla velocità angolare correnti, immaginando che queste rappresentino le condizioni iniziali delle oscillazioni libere che seguirebbero l'istante considerato se l'accelerogramma fosse troncato allo stesso istante. Le funzioni di ribaltamento così definite variano sulla durata dell'azione sismica e permettono di valutare quali siano i segmenti temporali più pericolosi nei confronti del ribaltamento.
In Figura 2.15 sono riportate le storie temporali della rotazione e delle funzioni di ribaltamento di un blocco con m = 6, p = 2.1996, e = 0.9595 soggetto all'accelerogramma di Sturno, ore 18:34 del 23/11/1980, componente N-S. Le storie temporali delle funzioni di ribaltamento hanno forme molto simili, a parte la "simmetria" dell'ETM rispetto alla DVA a al PVA. Durante le oscillazioni del blocco, l'ETM si avvicina al valore Y1 = 1, la DVA e il PVA al valore nullo, per poi tornare ai valori corrispondenti alla posizione di quiete, ossia: G = 1.0136, D = -0.363 rad/s, P = -0.137 rad2/s2.
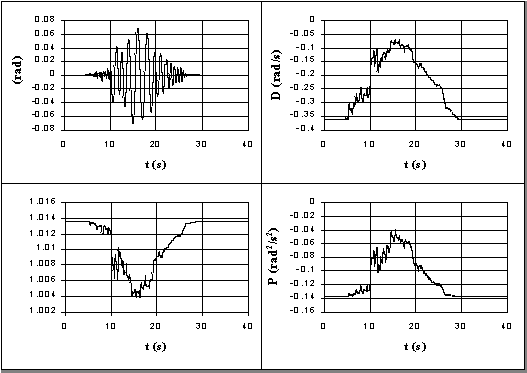
Fig. 2.15 - Storie temporali della rotazione e delle funzioni di ribaltamento per un blocco con µ = 6, p = 2.1996, e = 0.9595, soggetto all'accelerogramma di Sturno, ore 18:34 del 23/11/1980, componente N-S.
2.5 Funzionale di ribaltamento
Attraverso un'analisi della risposta di blocchi con
caratteristiche geometriche diverse alle accelerazioni di un dato terremoto, si
può giungere ad un quadro indicante quali di essi, in condizioni ideali,
subiscono il ribaltamento. Nessuna informazione si avrebbe, però, su quanto un
dato blocco che non è ribaltato, si è avvicinato a tale situazione o su quanto
rapidamente, un blocco ribaltato, sia arrivato a farlo. Una valutazione di
questo tipo può essere effettuata attraverso lo studio di funzioni che
esprimano la distanze in termini di rotazioni (q)
e velocità angolari (![]() ), istante per istante, tra i valori assunti e quelli,
), istante per istante, tra i valori assunti e quelli, ![]() e
e ![]() , che porterebbero il blocco al ribaltamento. Una funzione
così definita è, ad esempio, il Prodotto
in Velocità Angolare (PVA)
descritta in precedenza, che presenta un valore di soglia in corrispondenza di PVA = 0; per valori della funzione al di
sotto di esso, e quindi negativi, il blocco non ribalta, per valori del PVA positivi tende a ribaltare. Tanto
più, quindi, il PVA si è avvicinato
al valore di soglia durante la sollecitazione dinamica, pur senza superarlo,
tanto più il blocco ha "rischiato" il ribaltamento. Quanto prima, invece, per
un blocco si è superato il valore di soglia tanto più si può considerare
elevata la sua vulnerabilità a ribaltamento.
, che porterebbero il blocco al ribaltamento. Una funzione
così definita è, ad esempio, il Prodotto
in Velocità Angolare (PVA)
descritta in precedenza, che presenta un valore di soglia in corrispondenza di PVA = 0; per valori della funzione al di
sotto di esso, e quindi negativi, il blocco non ribalta, per valori del PVA positivi tende a ribaltare. Tanto
più, quindi, il PVA si è avvicinato
al valore di soglia durante la sollecitazione dinamica, pur senza superarlo,
tanto più il blocco ha "rischiato" il ribaltamento. Quanto prima, invece, per
un blocco si è superato il valore di soglia tanto più si può considerare
elevata la sua vulnerabilità a ribaltamento.
Per misurare, quindi, la vulnerabilità di più blocchi in corrispondenza di un certo sisma si può procedere, oltre che con un controllo diretto dell'eventuale ribaltamento, valutando di quanto, in media, il PVA si è avvicinato al valore di soglia, nel caso di blocco non ribaltato, o in che istante dall'inizio del sisma è avvenuto il ribaltamento, nel caso di blocco ribaltato.
Sulla base delle riflessioni appena fatte si è ritenuto indispensabile formulare un sintetico indice, capace - per un assegnato accelerogramma e per qualsiasi geometria del blocco rigido - di ordinare per vulnerabilità crescente situazioni di ribaltamento e non ribaltamento.
Tale indice, definito Funzionale di Ribaltamento ha, quindi, lo scopo di quantificare la tendenza di blocchi rigidi liberi di oscillare a ribaltare se sottoposti ad azione sismica.
In questa prima fase dello studio si è individuato il funzionale di ribaltamento relativo alla funzione PVA, ma un discorso analogo potrebbe essere fatto anche per le altre funzioni di ribaltamento precedentemente descritte.
La curva esprimente il PVA di ciascun blocco è caratterizzata da un valore costante iniziale dovuto alla fase in cui il blocco non ha ancora iniziato ad oscillare e dipendente dalle dimensioni geometriche del blocco. Per effettuare, quindi, un confronto corretto tra le curve del PVA rappresentative di ciascun blocco, si è scalato ciascun punto della curva per il valore costante che assume il PVA quando il blocco è in fase statica; in tal modo tutte le curve presentano una comune linea di base in corrispondenza di PVA = ǃ.
L'osservazione delle curve relative ai diversi blocchi ha permesso di definire un funzionale S dipendente dell'area A, sottesa dalla curva del PVA, e dalla ordinata d, del baricentro di A, rispetto all'asse dei tempi. La prima variabile (A) è indicativa della durata della fase di oscillazione dei blocchi e dei livelli massimi del PVA raggiunti in questa fase. Essa viene calcolata sommando le strisce di area comprese tra l'asse delle ordinate e il generico tratto di curva. Tra due punti consecutivi si può ottenere con la seguente espressione riferita alla Fig. 2.16:
![]()
In questo modo risultano positiva l'area delle fasce generate dai tratti crescenti della curva e negativa quella generata dai tratti decrescenti. Nel complesso, quindi, saranno positive le aree relative alle curve "aperte" proprie dei blocchi ribaltati (curva fucsia in Fig. 2.16) e negative quelle generate dalle curve "chiuse" dei blocchi non ribaltati (curva blu in Fig. 2.16).
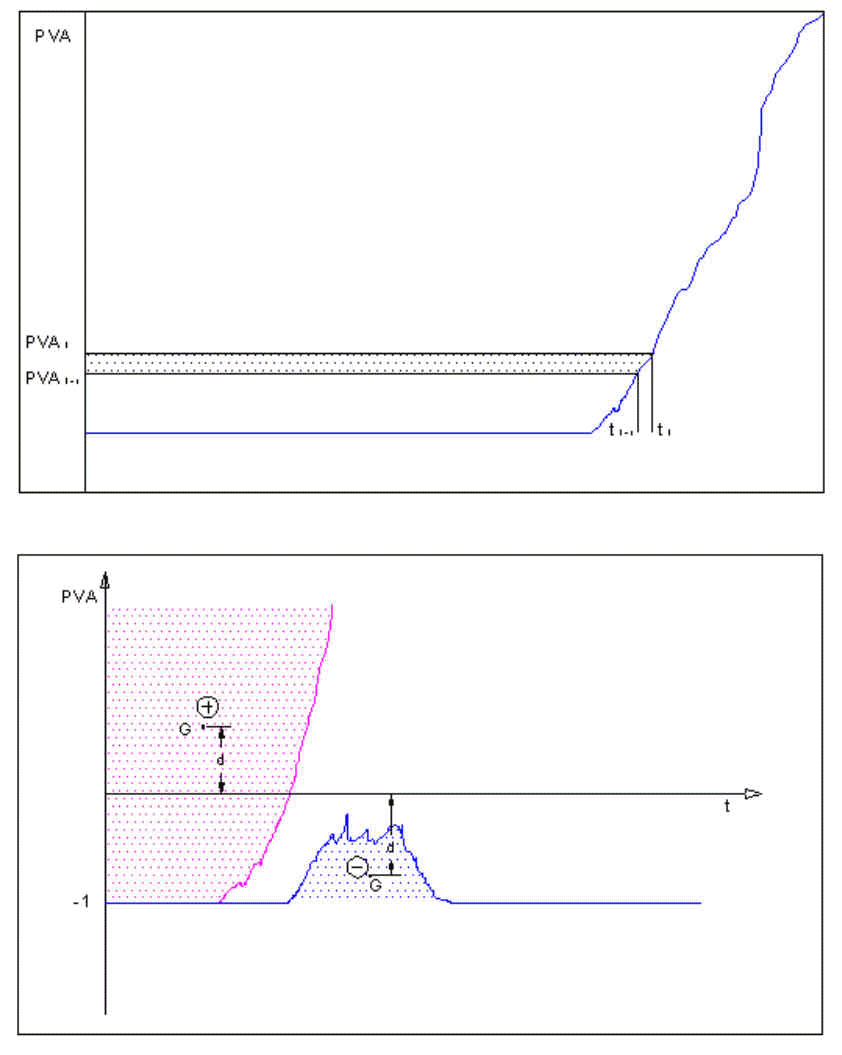
Fig. 2.16 - Definizione del funzionale utilizzato.
La seconda variabile d, indicata sempre in Fig. 2.16, ha, nell'ambito dei blocchi non ribaltati, lo scopo di esaltare l'influenza dei massimi valori raggiunti dal PVA, mentre, nei blocchi ribaltati, lega il valore del funzionale all'istante in cui avviene il ribaltamento.
In definitiva, il funzionale S rileva di quanto e per quanto tempo i blocchi non ribaltati si sono avvicinati alla situazione di ribaltamento, mentre attribuisce un diverso grado di pericolosità per i blocchi ribaltati a seconda dell'istante di ribaltamento, attribuendo un maggior valore, e quindi una maggiore vulnerabilità, a quelli ribaltati per primi.
Il funzionale descritto ha la seguente espressione:
![]()
con:
A = area sottesa dalla curva del Prodotto in Velocità Angolare rispetto alla linea di base rappresentata dal valore costante che il PVA assume quando il blocco è fermo;
d = ordinata del baricentro dell'area A rispetto all'asse dei tempi.
|
|
|
|
|
Fig. 2.17 - Chiesa Incompiuta di Venosa (PZ). |
||
2.5.1 Applicazione ad una colonna
dell'Incompiuta di Venosa
Quale ultima fase della ricerca condotta, si è affrontato lo studio di una colonna isolata della basilica Incompiuta di Venosa, in provincia di Potenza (Fig. 2.17).
Della Chiesa Nuova o Incompiuta (Larotonda 1999) non si conosce con esattezza l'anno di costruzione; la tesi più accreditata è quella del Bertaux, che ritiene la fondazione avvenuta tra il 1135 e il 1140. L'interno, con pianta a croce latina, presenta tre navate; la navata centrale è separata da quella di destra da cinque colonne, mentre quelle che avrebbero dovuto dividerla dalla navata sinistra non sono mai state erette. I capitelli delle colonne hanno forme dissimili tra loro e vari ornamenti: fogliame o figure bestiarie in stile romanico (Fig. 2.17). Nello studio condotto si è, tuttavia, presa in conto la colonna priva di capitello.
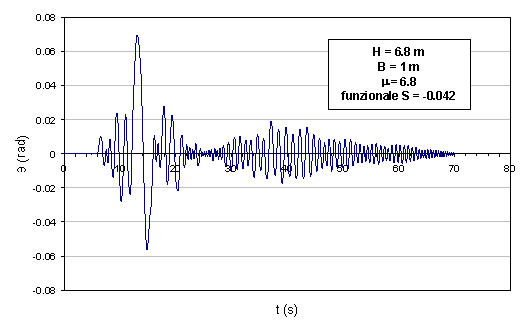
Fig. 2.18 - Oscillazioni della colonna sottoposta alla componente N-S del sisma dell'Irpinia.
La colonna, alta 6.8 m ed avente diametro di 1 m, è stata modellata come un unico blocco rigido ed è stata sottoposta ad una forzante dinamica rappresentata dalla componente Nord-Sud del sisma dell'Irpinia del 1980 (registrazione di Sturno).
La time history tracciata mediante l'analisi dinamica effettuata (Fig. 2.18) mostra come la colonna subisce delle rotazioni fino a 4° rispetto alla verticale nella fase più intensa del sisma, ma continua ad oscillare durante tutto l'evento, dissipando molto poco ad ogni impatto.
Considerando che la posizione di equilibrio instabile è contraddistinta da un angolo di circa 8° rispetto alla verticale, può concludersi che la colonna è abbastanza vicina al ribaltamento. Ciò è confermato dal valore del funzionale di ribaltamento S pari a ǂ.042, negativo - a segnalare il non ribaltamento - ma abbastanza vicino al valore di soglia 0 - ad indicare la vicinanza al ribaltamento.
A conferma di quanto detto, si è ritenuto utile effettuare una serie di analisi su blocchi di dimensioni differenti sottoposti alla stessa azione sismica. Quali parametri dell'indagine si sono assunte la snellezza m e la semilarghezza del blocco b: la prima è stata fatta variare tra 5 e 25 con incremento 0.1 (201 valori), la seconda tra 0.15 m e 1 m con incremento 0.05 m (18 valori). In totale sono state quindi effettuate 3618 elaborazioni.
Fig. 2.19 - Rappresentazione del Funzionale di
Ribaltamento per la componente N-S del Sisma dell'Irpinia (1980) al variare
della snellezza del blocco e della sua semilarghezza
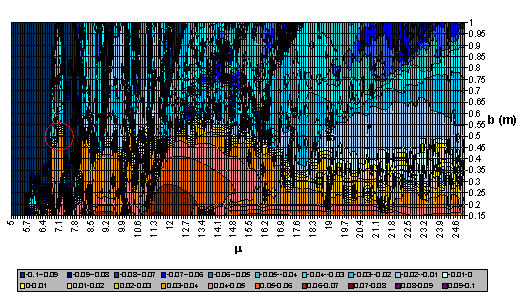
Fig. 2.19 - Rappresentazione del Funzionale di Ribaltamento per la componente N-S del sisma dell'Irpinia (1980) al variare della snellezza del blocco e della sua semi-larghezza.
2.6 Conclusioni
Le funzioni di ribaltamento presentate in questo studio derivano dall'analisi dei bacini di attrazione del blocco oscillante e permettono di stabilire se il blocco ribalta o meno nelle oscillazioni libere che seguono assegnate condizioni iniziali. Esse, inoltre, ordinano monotonicamente condizioni iniziali caratterizzate da tendenza al ribaltamento via via più marcata.
E' possibile estendere la definizione di funzione di ribaltamento al caso di un'azione sismica, calcolando a ogni istante il valore della funzione di ribaltamento corrispondente alla rotazione e alla velocità angolare corrente; esso rappresenta la tendenza del blocco al ribaltamento nelle oscillazioni libere che seguirebbero l'istante considerato se l'accelerogramma fosse troncato allo stesso istante. Le funzioni di ribaltamento variano nel tempo e permettono di cogliere i segmenti temporali più pericolosi ai fini del ribaltamento.
La funzione di ribaltamento Prodotto in Velocità Angolare è stata utilizzata per definire un funzionale, rappresentativo dell'intera storia temporale, che permette di quantificare con un solo valore numerico la vulnerabilità nei confronti del ribaltamento.
Quale esemplificazione dell'applicabilità a casi reali della trattazione condotta, si è studiata la risposta di una colonna dell'Incompiuta di Venosa (PZ) sollecitata dinamicamente; i risultati dimostrano come tale colonna sia in grado di sopportare il sisma dell'Irpinia del 23 novembre 1980 senza ribaltare.
è stata, infine, introdotta un'efficace rappresentazione del funzionale di ribaltamento, che permette di comprendere immediatamente la vulnerabilità a ribaltamento di un qualsiasi blocco rigido e libero di oscillare sottoposto al sisma irpino.
Giannini, R. & Masiani,
R. (1991): Risposta sismica del blocco
rigido. Atti del 5° Convegno Nazionale "L'Ingegneria Sismica in Italia": 491놼.
Housner, G.W. (1963): The
behaviour of inverted pendulum structures during earthquakes. Bulletin of
the Seismological Society of America 53(2): 403녩.
Larotonda, A.L. (1999): Potenza, una Provincia di cento Comuni. Amministrazione Provinciale di Potenza.